The study of logic involves carefully looking at the rules and steps that control good reasoning and inference. It also includes analyzing and assessing arguments, figuring out if statements are true or false, and following a structured process to reach reliable conclusions.
- FALSE = 0
- TRUE = 1
∧ and ∨
The symbol “∧” in logic represents the logical operator “conjunction,” which is also referred to as “AND.” In propositional logic, a logical conjunction connects two propositions and is true only when both of the connected propositions are true.
For example, if we have two propositions, P and Q, the conjunction of P and Q, denoted as P ∧ Q, is true only if both P and Q are true. If either or both of them are false, then the conjunction is false.
TRUTH TABLE:
| P | Q | P ∧ Q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
The symbol “∨” in logic represents the logical operator “disjunction,” which is also referred to as “OR.” In propositional logic, a logical disjunction connects two propositions and is true if at least one of the connected propositions is true.
| P | Q | P ∨ Q |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
⊻ (EXCLUSIVE OR)
The symbol “⊻” in logic is the “exclusive disjunction” or “XOR” operator. It connects two propositions and is true only when one of the connected propositions is true, but false when both are true or both are false.
| P | Q | P ⊻ Q |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
In logic, an “if” statement is a conditional statement that asserts a relationship between two propositions. The general form of an “if” statement is:
If
�
,
then
�If P, then Q
Here, �P is the antecedent (the “if” part) and �Q is the consequent (the “then” part). The statement asserts that if �P is true, then �Q must also be true.
If and Only If (Iff) Statement:
An “if and only if” (iff) statement is a biconditional statement that asserts a bidirectional relationship between two propositions. The general form of an “iff” statement is:
�
iff
�P iff Q
This statement means that �P is true if and only if �Q is true. It consists of two implications: �
→
�P→Q (if �P, then �Q) and �
→
�Q→P (if �Q, then �P).
Truth Tables:
To understand these concepts better, you can create truth tables. Truth tables help you analyze the truth values of propositions under different scenarios.
Let’s create a truth table for the “if” statement:
�
�
�
→
�
�
�
�
�
�
�
�
�
�
�
�
�PTTFFQTFTFP→QTFTT
And for the “iff” statement:
�
�
�
iff
�
�
�
�
�
�
�
�
�
�
�
�
�PTTFFQTFTFP iff QTFFT
Feel free to substitute different propositions for �P and �Q to see how the truth values change.
Examples:
If Statement:
�P: It is raining.
�Q: I will take an umbrella.
If it is raining, then I will take an umbrella.If it is raining, then I will take an umbrella.
Iff Statement:
�P: A shape is a square.
�Q: All angles are right angles.
A shape is a square iff all angles are right angles.A shape is a square iff all angles are right angles.
These examples illustrate how “if” and “iff” statements work in logic. Feel free to ask if you have any specific questions or if you’d like more examples!
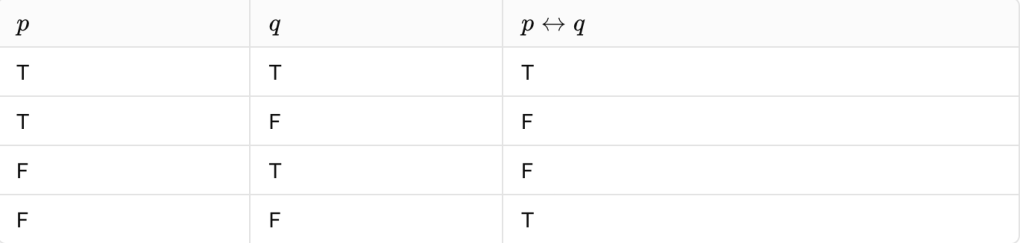
Sure, here’s how you can represent the “if and only if” symbol in logic:
Symbol: The symbol used for “if and only if” is ↔↔ (a double-headed arrow).
Meaning: In logic, �
↔
�p↔q means “if and only if” or “p is true if and only if q is true.” It indicates that the truth of �p is equivalent to the truth of �q.
Usage:
In mathematical logic, �
↔
�p↔q is often used to express biconditional statements, where both the implication �
→
�p→q and its converse �
→
�q→p hold true.
For example, �
>
2x>2 if and only if �
2
>
4x2>4, can be represented as �
>
2
↔
�
2
>
4x>2↔x2>4.
TRUTH TABLE:
Leave a comment